1.2 Some history and more motivation

(Konigsberg Problem. Euler, 1736)

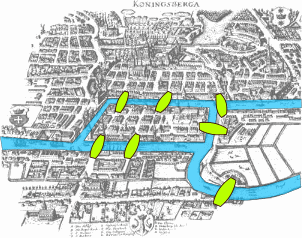
The problem was to find a path starting at any point that traverses through all the bridges exactly once and return to the starting point (See figure 1.10). After many attempts in vain, Euler showed that this is not possible. This problem is considered the birth of both probability and topology. We shall see Euler’s solution later.

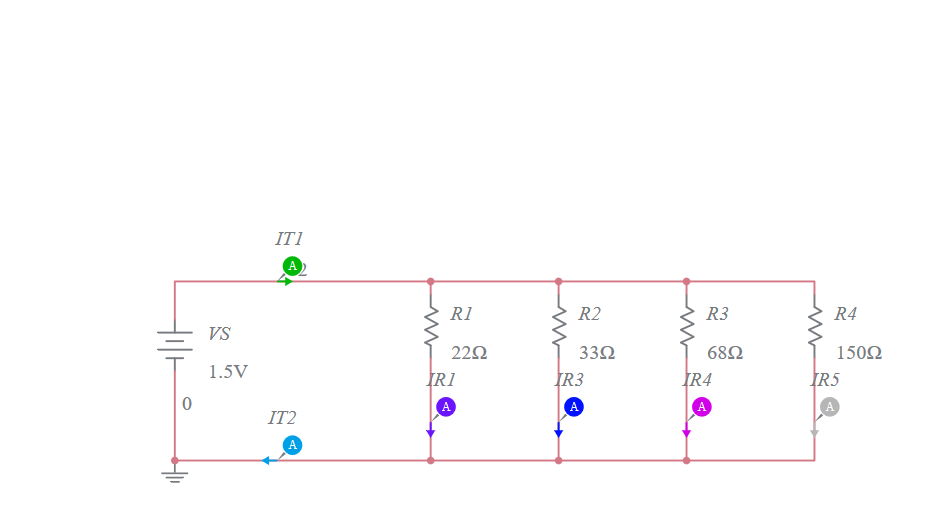
(Electrical Networks. Kirchoff, 1847) Electrical networks can be represented as weighted directed graphs with current and resistance viewed as weights; See Figure 1.11. This formalism can explain Kirchoff’s and Ohm’s laws. This connection between graphs and electrical networks is highly useful not only for graph theory and electrical networks but also used in random walks and algebraic graph theory. It is not entirely inaccurate to talk of Kirchoff’s formalism also as discrete cohomology.

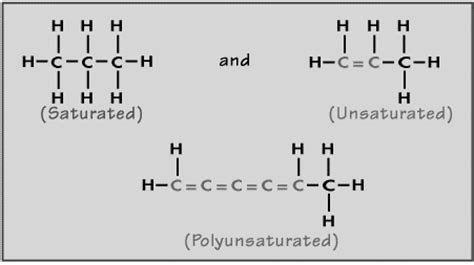
(Chemical Isomers. Cayley, 1857) Atoms were represented by vertices and bonds between atoms by an edge. Such a representation was used to understand the structure of molecules. We shall see Cayley’s tree enumeration formula which was used in enumeration of number of chemical isomers of a compound. See Figure 1.12.

(Tour of cities. Hamilton, 1859) Given a set of cities and roads between them, find a path that starts at one city, visits all the cities exactly once and returns to the starting city.

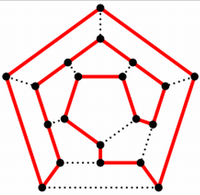
Can we guarantee such a path exists for all road networks ?

(Four colour theorem) Suppose we take a map of the world and assume that countries are contiguous land masses. Let countries be vertices and edges are drawn between two countries share a boundary. Can we colour countries such that neighbouring countries have different colours ? What is the minimum number of colours required for the same ?

A more general question, can any graph be drawn as a map i.e., can any graph be drawn on the plane such that edges do not cross each other ?

(A number theory graph) Here are two examples of graphs that were introduced towards a proof of Chowla’s conjecture. Define $G_m=(V_m=\{m,\mathrm{\dots },2m\},E_m)$ where are $n\sim n+p$ for a prime $p$ such that $p|n$ (i.e., $p$ divides $n$). The interest is in the number of walks of length $k$ (asymptotically in $k,m$) as $m\to \mathrm{\infty }$ and also eigenvalues of certain matrices associated to $G_m$. This was defined by T. Tao. To approximate this graph better, Helfgott and Radizwiłł  defined the following weighted graph. $G_m^{\prime }=(V_m==\{m,\mathrm{\dots },2m\},E_m^{\prime })$ where edges are $n\sim n+p$ for a prime $p$ and $w(n,n+p)=1/p$.

For a popular exposition on Chowla conjecture and this graph, see https://www.quantamagazine.org/mathematicians-outwit-hidden-number-conspiracy-20220103/ and [Helfgott 2022] for more details.