1 Introduction to Discrete Mathematics 1.2 Some history and more motivation 2 Some basic notions

1.3 Tentative Course overview :

Already, we have seen some historic questions that shall be discussed in the course. Now, we shall see something more specific that will be covered in the course.

1.3.1 Basic counting techniques

Initially we will recall basic counting techniques such as double counting principle, averaging principle, inclusion-exclusion and see their applications in graph theory. Then we shall discuss some basics regarding recursions and generating functions.

1.3.2 Flows, Matchings and Games on Graphs

Example 1.17 (Maximum traffic flow).

Consider the traffic network (weighted graphs) and take a starting point (source) and ending point (sink). What is the maximum amount of traffic that can flow from source to the sink in one instance ?

The solution is very famously known as the max flow-min cut theorem and has many applications.

Example 1.18 (Hostel room allocation).

There are $n$ rooms and $m$ students. Each student gives a list of rooms acceptable to them. Can the warden allot rooms to students such that each student gets at least one room in their list ?

Hall’s marriage theorem shall give a deceptively simple sufficient and necessary condition for the same. Hall’s marriage theorem shall be proved using max flow-min cut theorem.

Example 1.19 (Hide and Seek game).

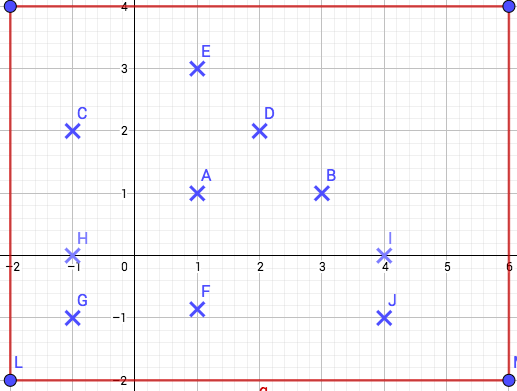
Refer to caption — Figure 1.14: An example of a hide and seek scenario.

Consider an area with horizontal main roads and vertical cross roads (See the grid in Figure 1.14). There are safe houses at certain intersections, marked by crosses in the figure. A robber choses to hide at one of the safe houses. A cop wants to find the main road or the cross road in which the robber stays. What is the best strategy for the cop to succeed ? What is the best strategy for robber to defeat the cop ? We shall exhibit a strategy for both using Hall’s marriage theorem.

1.3.3 *Graphs and matrices

A graph $G$ on $V$ can be represented as a $V\times V$ matrix with $1$ in the column $(v,w)$ iff $(v,w)$ is an edge in $G$ . One can represent weighted and directed graphs as well. What does rank and nullity mean here ? Are there other matrices that encode the properties of graphs ? This viewpoint shall connect Kirchoff’s formalism with cohomology theory. We may not be able to cover it in the course.

1.3.4 Random graphs and probabilistic method.

If time permits, we shall mention random graphs. We fix $[n]$ as the vertex set and choose edges at random i.e., at each edge toss a coin and place the edge if it lands heads. What are the properties of these graphs ?

Probabilistic method : Suppose we want to show that there exists graphs with a certain property, let us show that the random graph satisfies the property with positive probability. Thus, the set of graphs satisfying the property is non-empty. This approach was pioneered by Erdös and is still remarkably successful in proving various results.

I shall try to emphasize various mathematical topics (such as cohomology) that show up in their simplest incarnation in graph theory and also, many mathematical tools such as linear algebra, analysis and probability are used to study graphs. A very readable survey on the growing importance of graph theory is [Lovasz 2011].