13.3 ***Graph dual****

Let $G$ be a plane graph. Construct a new (multi-) plane graph $G^{\ast }$ called the dual as follows : Choose $x_i\in {\mathring{F}}_i$ for all faces $F_i$’s. For all $e\in \partial F_i\cap \partial F_j$ for $i\ne j$, draw an edge between $x_i$ and $x_j$. If $e\in \partial F_i$ is a cut-edge, we draw a loop at $x_i$. We can draw $G^{\ast }$ as a plane graph as follows : Connect $x_i$ to the mid-point of all edges $e$ such that $e\in \partial F_i$ such that paths to no two edges intersect. Thus, if $e\in \partial F_i\cap \partial F_j$ for $i\ne j$ then $x_i$ and $x_j$ are connected to mid-points of $e$. If $e$ is a cut-edge, draw two non-intersecting edges to mid-point of $e$.

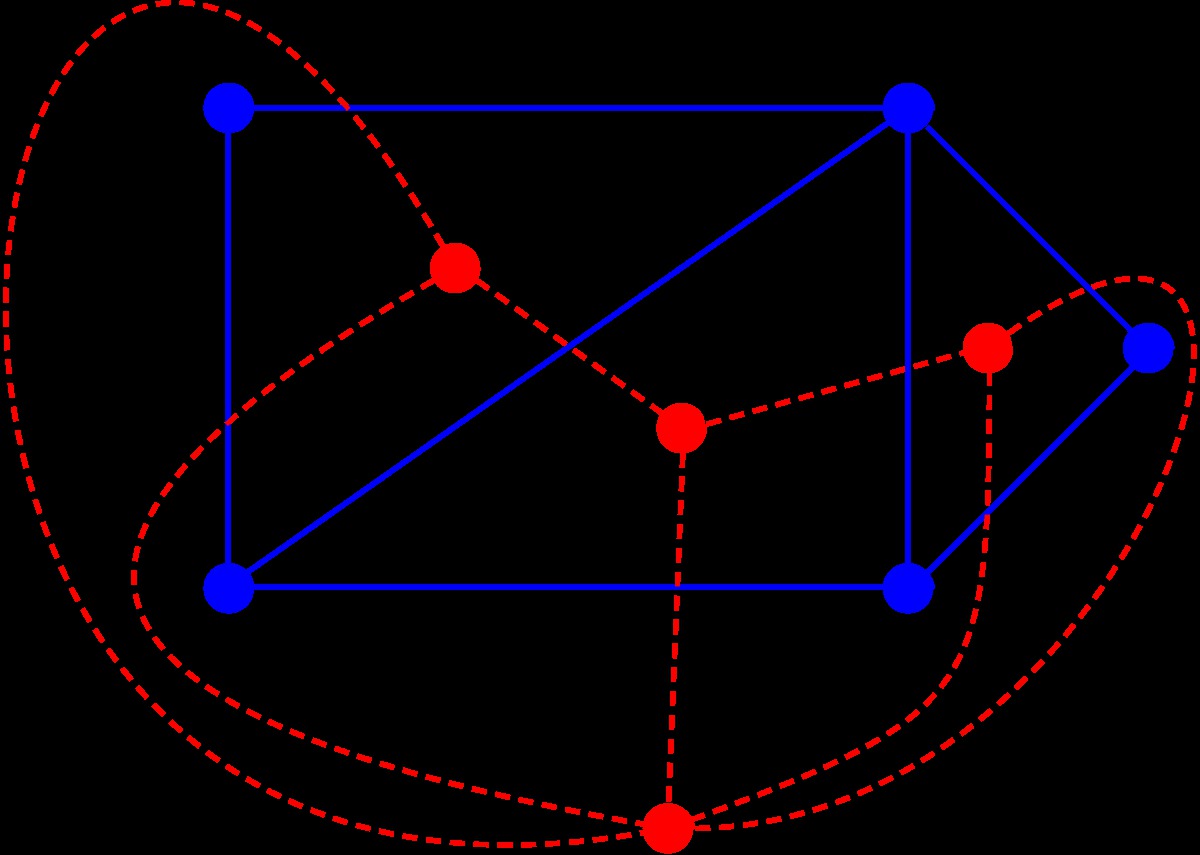
For example, see the Figure 13.1 for a graph (blue) and its dual (in red).

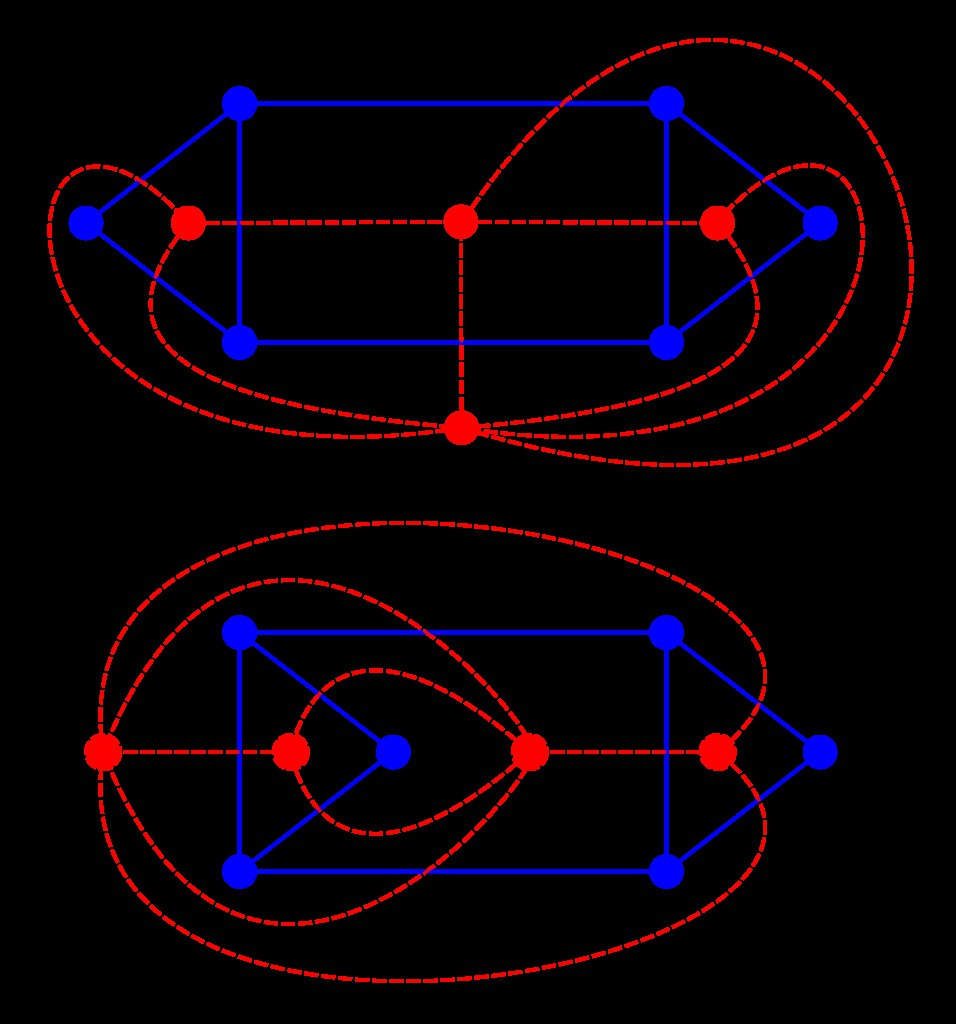
Two isomorphic graphs can have different duals. See Figure 13.2.

Hint : Show that $d_{G^{\ast }}(x_i)=l(F_i).$